Bodenkennwerte
Bodenkennwerte
Nachweis ihrer Berechenbarkeit
Für die Kennzeichnung von Böden, Benennung, Klassifikation und Belastung sind nach unterschiedlichen Gesichtspunkten DIN- und EN-Normen geschaffen worden, wie:
- DIN 1054 / EC/7, DIN 4020 bis DIN 4023, DIN 4030, DIN 18196, DIN 18300, DIN 19682-1+2, DIN 19682-2, DIN 19682-12, DIN EN 1997-1, DIN EN ISO 14688-1, DIN EN ISO 14688-2, DIN EN ISO 14689-1 und andere.
Vorwiegend werden in diesen Normen Böden nach magmatischen, metamorphen oder sedimentären Ursprungsgesteinen, nach nichtbindigen und bindigen Böden sowie nach Kornform und Kornrauigkeit, Tragfähigkeit und Setzungsverhalten unterteilt. Im wesentlichen stützen sich die daraus entwickelten Bodenkennwerte auf empirisch gefundene Basiswerte. Für Erddruckberechnungen hat Herr Prof. Dr. Rolf Katzenberg, Institut und Versuchsanstalt für Geotechnik der TU-Darmstadt die Unzahl von Kagh-Werten in Tabellen zusammengefasst, Abb. 1.
Abb.: Studienunterlagen Geotechnik, TU Darmstadt – Anlage VI-2 – Erddruck vom 10.03.2014
Zu den Tabellenwerten ist anzumerken, augenscheinlich mögen diese für Aufsteller von Erddruckberechnungen hilfreich sein, doch sie offenbaren auch ihre negativen Einflüsse:
- Alle Bodenwerte sind empirisch, sie haben keinen direkten Bezug zur anstehenden Bodenart.
- Die Vielzahl der Tabellenwerte erlaubt dem Aufsteller Kenngrößen frei zu wählen. Damit wird es ihm erlaubt Werte zu verwenden, die sein Bauvorhaben in einen günstigeren Kostenrahmen zu versetzen.
- Gleichermaßen ermöglicht die Vielzahl der Tabellenwerte Gutachtern bei einem Schadensfall Versäumnisse frei, d.h. ohne sachlichen Bezug der einen oder anderen Partei zuzuweisen.
Die Neue Erddrucklehre setzt auf die Berechenbarkeit realer Bodeneigenschaften und benötigt keinerlei empirischer Zufallswerte. Eigene umfangreiche labortechnische Untersuchungen trockener, feuchter und nasser Böden sowie von Böden unter Wasser offenbarten, dass jede Bodenart unverwechselbare Eigenschaften aufweist. Werden Böden durch natürliche oder künstliche Eingriffe gestört, so bilden sich neue Bodenarten mit eigenen Eigenschaften. Den Berechnungsweg gibt das Mehrphasensystem der Festkörperphysik vor. Grundlage der Berechnungen bilden labortechnische Untersuchungen gezogener Bohrkerne sowie ungestörter Bodenproben. Daraus ermittelt werden können alle relevanten Werte für den Erddruck, die Tragfähigkeit und das Setzungsverhalten von Böden.
Für die Berechnungen der Bodeneigenschaften werden Annahmen getroffen und die Bodendichten mit der Einheit t/m³ angesetzt:
- Als Volumen der Erdmasse wird Vp = 1,00 m³ festgelegt. Dieses unterteilt sich in der Regel in das Festkörpervolumen Vf und in das Porenvolumen Vl.
- Nur das Porenvolumen Vl kann sich teilweise oder auch vollständig mit Flüssigkeit / Wasser füllen, wobei angenommen wird, dass Poreneinschlüsse im Gestein kein Wasser aufnehmen, also trocken bleiben.
- Bei nassen Böden wandelt sich das Porenvolumen von Vl nach Vln.
- Bei feuchten Böden besetzt das anstehende Wasser nur teilweise das Porenvolumen Vl, wobei das mit Wasser gefüllte Vl sich zum Volumen Vli wandelt.
- Bei den Dichten nimmt den oberen Platz in der Bodenskala das harte Felsgestein / Granit ein mit der Dichte y90 = 29,42 kN/m³ gleich ptg90 = 3,0 t/m³ (ptg = neue Bezeichnung) mit Vp = Vf = 1,00 m³;
- Den unteren Platz in der Bodenskala nimmt der Urstaub ein (neue Bezeichnung) mit der Bodendichte ptg0 = 0,03 t/m³ mit Vf = 0,01 m³;
- Dichte der Flüssigkeit / Wasser pwg = 1,00 t/m³ (pwg = neue Bezeichnung).
Symbolzeichen finden sich im Buch „Die neue Erddrucklehre auf den reinen Grundlagen der Physik“.
Aus dem gezogenen Bohrkern sowie der ungestörten Bodenprobe sind unter labortechnischen Bedingungen folgende Werte zu ermitteln:
- Gewicht der ungestörten Bodenprobe bei bekanntem Volumen;
- Gewicht der getrockneten Bodenprobe;
- Gewicht der Bodenprobe nach vollständiger Auffüllung mit Wasser;
- Anpassung von Volumen und der jeweils gewogenen Gewichts an das Volumen Vp = 1,00 m³, ergeben die Dichten ptg (trocken), pig (feucht) und png (nass) in der Einheit t /m³.
Umfangreiche Versuche zum Bodenverhalten sind durchgeführt. Sie bestätigten die Lage der Neigungs- und Scherebene von Böden gemäß den Abb. 2 und 3, siehe eigene Studie.
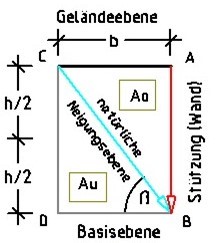
Abb. 2 zeigt die Keilflächen Ao und Au, die durch die Neigungsebene mit dem Winkel β getrennt werden.
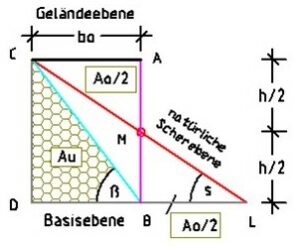
Abb. 3 zeigt den ‚liegenden Erdkeil’(C–L–D), die Neigungsebene und die Scherebene unter dem Winkel s.
Nachstehende Beispiele bestätigen, dass Bodenkennwerte berechenbar sind:
Beispiel 1: Ermitteltes Gewicht der trockenen Bodenmasse F = 1,765 t, Abb. 4.
Aus dem Trockengewicht F der Bodenprobe ist zunächst die Bodendichte ptg mit der Einheit t / m³ und danach das Feststoffvolumen Vf und das Porenvolumen Vl = Vli zu ermitteln. Hierbei wird davon ausgegangen, dass sich das Gesamtvolumen Vp zusammensetzt aus Vp = Vf + Vl und das Porenvolumen Vl = Vlt mit Gas / Luft mit der Dichte mit 0,0 t/m³ besetzt ist. Aus dieser Abhängigkeit errechnen sich das Feststoffvolumen Vf = F / ptg90 = 1,765 / 3,0 = 0,588 m³ und das Porenvolumen = Vp – Vf = 1,000 – 0,588 = 0,412 m³.
Der Neigungswinkel ßt lässt sich über das Verhältnis Vli / Vf errechnen, tan ßt = Vf / Vli = 0,588 / 0,412 = 1,427 ⟶ ßt = 55,0°. Der Scherwinkel bildet sich aus tan st = tan ßt /2 = 1,427 /2 = 0,714 ⟶ st = 35,5°.
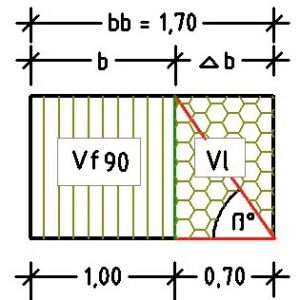
Das gleiche Ergebnis stellt sich ein beim Erdband (Abb. 4). Hier errechnet sich der Winkel ßt über das Verhältnis der Volumina der festen Gesteinsmasse Vf90 = 1,00 m³ und dem fiktiven Porenvolumen Vl = h ∙ a ∙ ^b, wobei sich die Breite ^b = Vl / = 0,412 / 0,588 = 0,70 m darstellt. Oder Neigungswinkel tan ßt = h / ^b = 1,0 / 0,70 = 1,427 ⟶ ßt = 55,0°.
Abb. 4: Erdband ohne Wasseranteil
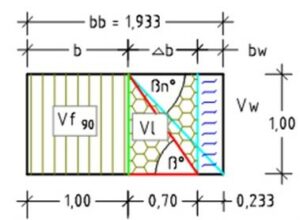
Abb. 5: Erdband mit Wasservolumen Vw
Beispiel 2: Ermitteltes Gewicht der trockenen Bodenmasse F = 1,765 t, Porenvolumen Vln = 0,412 m³, d. h. das Porenvolumen hat sich vollständig mit Wasser aufgefüllt, Abb. 5.
Das Gewicht des Erdbands (Abb. 4) erhöht sich durch die Wasserzugabe (Abb. 5) auf F‘ = Vf ∙ ptg90 + Vln ∙ pwg = 1,00 ∙ 3,0 + 0,70 ∙ 1,00 = 3,700 t. Normiert man dieses Gewicht auf das Würfelvolumen Vp = 1,00 m³, erhält man F“ = F‘ ∙ b / (b + bw) = 3,70 ∙ 1,00 / (1,70) = 2,176 t. Über den Erdwürfel errechnet sich die Nassdichte png = Vf ∙ ptg90 + Vln ∙ pwg = 0,588 ∙ 3,00 + 0,412 ∙ 1,00 = 2,176 t/m³
Bei der Winkelberechnung ist zu berücksichtigen, dass ein nasser Boden schneller als ein trockener Boden abgleitet, d.h. der Neigungswinkel des nassen Bodens verringert sich. Folglich sind vorab das Wasservolumen Vw und seine Breite bw zu ermitteln. Das Wasservolumen ergibt sich aus dem Ansatz Vw = pwg ∙ (^b ∙ h ∙ a ) / ptg90 = 1,0 ∙ (0,70 ∙ 1,0 ∙ 1,0) / 3,0 = 0,233 m³ und nimmt die Breite bw = 0,233 m ein.
Der Neigungswinkel errechnet sich tan ßn = h /(^b + bw) = 1,0 / (0,70 + 0,233) = 1,072 ⟶ ßn = 47,0°. Der Scherwinkel stellt sich ein: tan sn = tan ßn /2 = 1,072 /2 = 0,536 ⟶ Scherwinkel sn = 28,2°.
Beispiel 3: Ermitteltes Gewicht der trockenen Bodenmasse F = 1,764 t (Abb. 4) plus gemessenes Wasser in Höhe von 8% oder Wasservolumen Vw = 80 Liter pro m³.
Das Erdband des trockenen Bodens (Abb. 4) verbreitert sich durch das aufgenommene Wasser um das Volumen Vli = (Vf + Vl) ∙ 8% = 1,70 ∙ 0,08 = 0,136 m³ bzw. um die fiktive Breite bw = Vli / h ∙ a = 0,136 / 1,0² = 0,136 m. Zudem erhöht das Wasser das Gewicht des Erdbands (Abb. 4) auf F*= Vf ∙ ptg90 + Vli ∙ pwg = 1,00 ∙ 3,0 + 0,136 ∙ 1,00 = 3,136 t. Dieses Gewicht auf das Würfelvolumen Vp = 1,00 m³ normiert bringt F* = F‘ ∙ b / (b + bw) = 3,136 ∙ 1,00 / (1,70) = 1,844 t bzw. die Feuchtdichte pig = Vf ∙ ptg90 + Vli ∙ pwg = 0,588 ∙ 3,00 + 0,080 ∙ 1,00 = 1,844 t/m³.
Wie vorgestellt, verändert das Wasser den Neigungswinkel ßt des trockenen Bodens hin zum Neigungswinkel ßi des feuchten Bodens. Über den Erdwürfel errechnet sich das Volumen Vli = 0,080 m³ und damit die Breite bw = Vli / h ∙ a = 0,08 / 1,0 ∙ 1,0 = 0,08 m. Damit stellen sich der Neigungswinkel ßi und der Scherwinkel si ein: tan ßi = Vf / (Vl + Vli / ptg90) = 0,588 / (0,412 + 0,080 /3) = 1,340 ⟶ ßi = 53,3° und Scherwinkel tan si = tan ßi /2 = 1,340 /2 = 0,670 ⟶ si = 33,8°.
Beispiel 4: Ermitteltes Gewicht der trockenen Bodenmasse F = 1,764 t (Abb. 4) plus gemessenem Wasser Vw = 200 Liter Wasser (20% Feuchte).
Das Beispiel soll die Gefahr eines Bergrutsches aufzeigen, der sich durch eine weitere Wasseraufnahme von 80 + 120 = 200 Liter einstellen kann.
Die Bodeneigenschaften werden über den Erdwürfel Vp = 1,0 m³ berechnet.
Wasservolumen Vli = 0,08 + 0,120 = 0,200 m³, Breite bw = Vli / h ∙ a = 0,20 / 1,0 ∙ 1,0 = 0,20 m. Feuchtdichte pig = Vf ∙ ptg90 + Vli ∙ pwg = 0,588 ∙ 3,00 + 0,20 ∙ 1,00 = 1,964 t/m³.
Der Neigungswinkel des feuchten Bodens errechnet sich: tan ßi = Vf / (Vl + Vli / ptg90) = 0,588 / (0,412 + 0,200 /3) = 1,228 ⟶ ßi = 49,4°.
Der Scherwinkel stellt sich ein bei tan si = tan ßi /2 = 1,228 / 2 = 0,614 ⟶ si = 31,5°.
Fazit
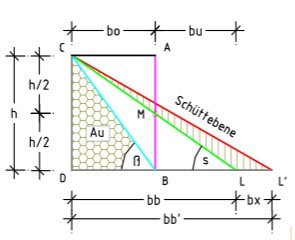
Bei einer Böschungshöhe h = 10 m verschiebt das von Boden zusätzlich aufgenommene Wasser den Böschungsfuß des leicht feuchten Bodens (Beispiel 3) um die Breite bx = ho ∙ (tan 1,340 – tan 1,228) = 10 ∙ 0,112 = 1,12 m. Das Berechnungsbeispiel bestätigt, dass sich nach Neuer Erddrucklehre Bergrutsche im Voraus berechnen lassen!
Abb. 6: Bildung der neue Schüttebene C-L‘ durch die zusätzliche Aufnahme des Bodens von Wasser.